Given the equation:
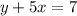
we can find its slope if we write it in the y=mx+b form:
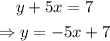
Now, we know as a general rule, that the slope of the perpendicular of the line that has slope m, is -1/m, more clearly:

So, in this case we have:
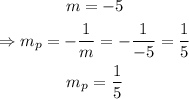
now we use the slope-point formula to find the equation of the perpendicular line:
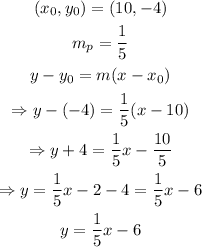
therefore, the line perpendicular to y+5x=7 that passes through (10,-4) is y=1/5x-6