Question

The figure shows the layout of a symmetrical pool in a water park. What is the area of this pool rounded to the tens place? Use the value = 3.14.

Answer 1

Step-by-step explanation:

Given;

We are given a symmetrical pool as indicated in the attached picture.

The pool consists of two sectors and two triangles and each pair has the same dimensions.

The dimensions are as follows;

`\begin{gathered} Sector: \\ Radius=30 \\ Central\text{ }angle=2.21\text{ }radians \end{gathered}`
`\begin{gathered} Triangle: \\ Slant\text{ }height=30 \\ Vertical\text{ }height=25 \\ Base=20 \end{gathered}`

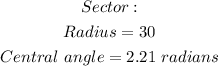
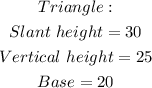
Required;

We are required to calculate the area of the pool.

Step-by-step solution;

We shall begin by calculating the area of the sector and the formula for the area of a sector is;

`\begin{gathered} Area\text{ }of\text{ }a\text{ }sector: \\ Area=(\theta)/(2\pi)*\pi r^2 \end{gathered}`

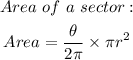
Where the variables are;

`\begin{gathered} \theta=2.21\text{ }radians \\ r=30 \\ \pi=3.14 \end{gathered}`

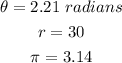
We now substitute and we have the following;

`Area=(2.21)/(2\pi)*\pi*30^2`
`Area=(2.21)/(2)*900`
`Area=994.5ft^2`

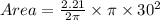
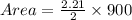
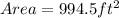
Since there are two sectors of the same dimensions, the area of both sectors therefore would be;

`Area\text{ }of\text{ }sectors=994.5*2`
`Area\text{ }of\text{ }sectors=1989ft^2`

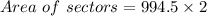
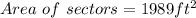
Next we shall calculate the area of the triangles.

Note the formula for calculating the area of a triangle;

`\begin{gathered} Area\text{ }of\text{ }a\text{ }triangle: \\ Area=(1)/(2)bh \end{gathered}`

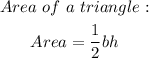
Note the variables are;

`\begin{gathered} b=20 \\ h=25 \end{gathered}`

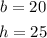
The area therefore is;

`Area=(1)/(2)*20*25`
`Area=(20*25)/(2)`
`Area=250`

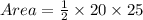
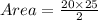
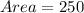
For two triangles the area would now be;

`Area\text{ }of\text{ }triangles=250*2`
`Area\text{ }of\text{ }triangles\text{ }equals=500ft^2`

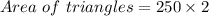
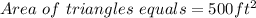
Therefore, the area of the pool would be;

`\begin{gathered} Area\text{ }of\text{ }pool: \\ Area=sectors+triangles \end{gathered}`
`\begin{gathered} Area=1989+500 \\ Area=2489ft^2 \end{gathered}`

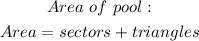
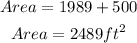
Rounded to the tens place, we would now have,

ANSWER:

`Area=2,490ft^2`

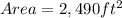
Option D is the correct answer