Diagonals of a parallelogram bisect each other.
The opposite sides of a parallelogram are parallel and equal.
In a triangle, the larger angle has a longer opposite side and a smaller angle has a shorter opposite side.
Law of cosine: If a, b, c are three sides of a triangle and A is the angle opposite to the side a, then
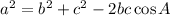
The diagonals of a parallelogram are 56 inches and 34 inches. They bisect each other and form 4 triangles.
Let ABCD is a parallelogram and the diagonals AC and BD intersect each other at point O.
AB parallel to CD , AB=CD.
BC parallel to AD , BC=AD.
Diagonals intersect at an angle of 130 degrees.
m∠AOD=120 degree.
BD is a straight line. So,
m∠AOD+m∠AOB=180 degree
120+m∠AOB=180 degree
∠AOB =180-120=60 degree.
The opposite side of 130∘, (AD and BC) are the longer sides and the opposite side of 60∘, (AB and CD) are the shorter sides.
Use the law of cosine in triangle AOB,
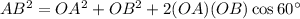

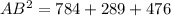

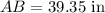
The length of shorter side is AB =39.35 in.