9514 1404 393
Answer:
x ≈ -0.5416
Explanation:
As with any "solve for ..." problem, you essentially want to "undo" what has been done to the variable of interest. Here, if you were to evaluate the left-side expression (where the variable is) for some value of x, you would ...
- multiply by 10
- add 7
- raise 9 to that power
- multiply by 2
- add 5
You want to "undo" these operations in reverse order. That is, you work from the bottom of this list toward the top, using inverse operations along the way.
The inverse of addition is subtraction; the inverse of multiplication is division. The inverse of raising to a power is taking a logarithm.
undo add 5
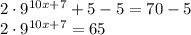
undo multiply by 2
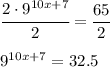
undo raise to a power (take logarithms)
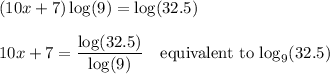
undo add 7
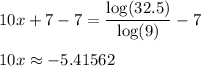
undo multiply by 10
