Answer:
k = -1
Explanation:
The limit will exist if:
One of the roots of the equation in the numerator is 5. This happens because if this happens, we can simplify with the denominator. So
Solving a quadratic equation:
In the following format:
ax² + bx + c = 0
The solution is given by:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
In this question:
x² + kx - 20 = 0
The solution is:
![x=\frac{-k\pm\sqrt[]{k^2-4\ast1\ast(-20)}}{2}=\frac{-k\pm\sqrt[]{k^2-80}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/xk32m0vcsootouylume340xa1jav8mi899.png)
Since we want x = 5.
![\frac{-k+\sqrt[]{k^2+80}}{2}=5](https://img.qammunity.org/2023/formulas/mathematics/college/8fv289uzbcehfqaame0afloafj7qmajbcb.png)
![-k+\sqrt[]{k^2-80}=10](https://img.qammunity.org/2023/formulas/mathematics/college/z2mjnrlevpowsb7r97p7pgir6l3m2bhvga.png)
![\sqrt[]{k^2+80}=10+k](https://img.qammunity.org/2023/formulas/mathematics/college/otfv8h23toh9ebcbcz2n8qqystdekrw6jt.png)
![(\sqrt[]{k^2+80})^2=(10+k)^2](https://img.qammunity.org/2023/formulas/mathematics/college/d003my6b10eq7hn4onko8bv0o8i4cb2jpy.png)
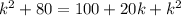
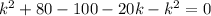
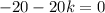
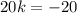
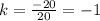
k = -1