Answer:
The point of intersection would be (3,-2)
Explanation:
To determine the intersection of the conics we can use a system of equations since they intersect when they are both equal.
Then, we have these equations:
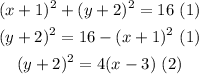
Equalize equations (1) and (2).
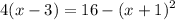
Solve for the x-coordinate.
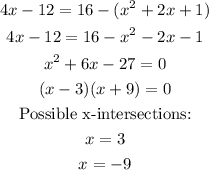
Since the circle has a radius of 4, we know that the intersection cannot be x=-9. Then, the x-coordinate to use is x=3.
Substitute x=3 into one of the equations to determine the y-coordinate:
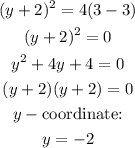
Hence, the point of intersection would be (3,-2)