Question

Elaine drives her car 50 miles and has an average of a certain speed. If the average speed had been 4mph more, she could have traveled 58 miles in the same length of time. What was her average speed?

Answer 1

Hello there. To solve this question, we'll have to remember some properties about average speed.

When we're talking about moving in a straight line, the average speed is given by the ratio between the displacement ΔS and the interval of time Δt, namely

`v=(ΔS)/(Δt)`

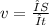
In this case, say we have an average speed of v and the initial displacement ΔS = 50 miles in a certain interval of time Δt, such that

`v=(50)/(Δt)`

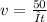
We know that if the average speed had been 4 mph more, then Elaine could have traveled 58 miles in the same length of time.

This means that v + 4 (that is, the average speed plus 4 mph) is equal to the ratio:

`v+4=(58)/(Δt)`

To solve this for v, we can start assuming that the interval of time Δt is not equal to zero, so do the average speed in the second equation.

Divide the first equation by the second, such that

`\begin{gathered} (v)/(v+4)=((50)/(Δt))/((58)/(Δt)) \\ \\ (v)/(v+4)=(50)/(58) \end{gathered}`

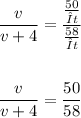
Cross multiply the numbers, that is:

`\begin{gathered} 58v=50\cdot(v+4) \\ 58v=50v+200 \end{gathered}`

Subtract 50v on both sides of the equation

`8v=200`

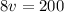
Divide both sides by a factor of 8

`v=25\text{ mph}`

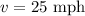
So this is her average speed.