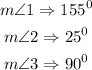To begin answering the question, let us familiarize ourselves with some basic terms
Linear Pairs: Two adjacent angles are a linear pair when their noncommon sides are opposite rays.
If you know the measure of one angle in a linear pair, you can find the measure of the other because the sum of the measure of the two angles is 180 degrees.
Vertical angles: Vertical angles are a pair of opposite angles formed by intersecting lines.
Vertical angles are equal.
We can now apply this knowledege to find the required angles
To find the measure of angle 1 (m<1)
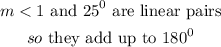
This means that
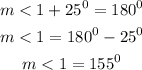
Thus, m<1 = 155°
To find the measure of angle 2 (m<2)
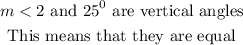
Hence,
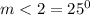
m<2 =25°
To get the measure of angle 3 (m<3)
Given: Line t is perpendicular to s
Wehen two lines are perpendicular to eachother, they meet at right angle
This means that
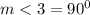
Thus,
m<3=90°
Hence, the summary of the solution is shown below