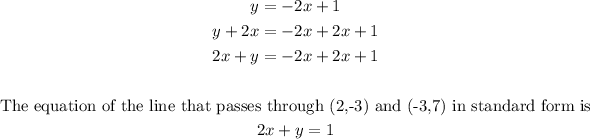Question

Hello could you please help me with this problem. Write and equation in standard form of the line that passes through (2,-3) and (-3,7).

Answer 1

Given:

point (2,-3) and (-3,7)

First, solve for the slope of the line

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ \text{substitute} \\ (x_1,y_1)=(2,-3) \\ (x_2,y_2)=(-3,7) \\ \\ m=(y_2-y_1)/(x_2-x_1) \\ m=(7-(-3))/(-3-2) \\ m=(7+3)/(-5) \\ m=(10)/(-5) \\ m=-2 \end{gathered}`

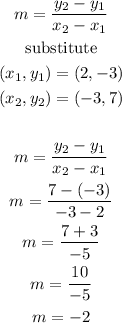
Now that we have solved for the slope, substitute it to the slope-intercept form y = mx + b to find the y-intercept. Use the point (2,-3) but using (-3,7) works just as well.

`\begin{gathered} y=mx+b \\ -3=(-2)(2)+b \\ -3=-4+b \\ -3+4=b \\ b=1 \end{gathered}`

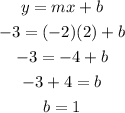
The slope intercept form of the line is

`y=-2x+1`

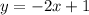
Rearrange it to follow the standard form Ax + By = C, and we have

`\begin{gathered} y=-2x+1 \\ y+2x=-2x+2x+1 \\ 2x+y=\cancel{-2x+2x}+1 \\ \\ \text{The equation of the line that passes through (2,-3) and (-3,7) in standard form is} \\ 2x+y=1 \end{gathered}`