Question

Consider the quadratic function.What are the x-intercepts and y-intercept?What is the equation of the axis of symmetry?What are the coordinates of the vertex?Graph the function on the coordinate plane. Include the axis of symmetry.

Answer 1

Kindly check below

1) Let's do it in parts.

a) We can find the x-intercepts by using the factor zero property from each factor. Like this:

`\begin{gathered} -(x+4)=0\Rightarrow-x-4=0\Rightarrow-x=4\Rightarrow x=-4 \\ (x-1)=0\Rightarrow x=1 \end{gathered}`

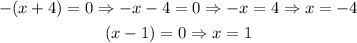
The best way to find the y-intercept with this factored form is by plugging into that equation x=0

`\begin{gathered} f(x)=-\left(x+4\right)\left(x-1\right) \\ y=-\left(x+4\right)\left(x-1\right) \\ y=-(0+4)(0-1) \\ y=-(4)(-1) \\ y=4 \end{gathered}`

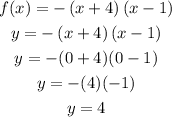
b) Expanding those factors by distributing them (FOIL) we can find this:

`\begin{gathered} f(x)=-\left(x+4\right)\left(x-1\right) \\ f(x)=-\left(xx+x\left(-1\right)+4x+4\left(-1\right)\right) \\ f(x)=-x^2-3x+4 \end{gathered}`

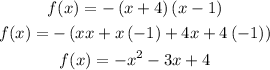
So now, let's find the x-coordinate of the vertex V(h,k):

`\begin{gathered} h=(-b)/(2a)=(-(-3))/(2(-1))=(3)/(-2)=-(3)/(2) \\ Axis\:of\:symmetry:x=-3/2 \end{gathered}`

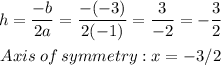
c) The coordinates of the vertex can be found by plugging the x-coordinate into the quadratic function. This way:

`\begin{gathered} f(x)=-\left(x+4\right)\left(x-1\right) \\ f(-(3)/(2))=-(-(3)/(2)+4)(-(3)/(2)-1)=(25)/(4) \\ \\ V(-(3)/(2),(25)/(4)) \end{gathered}`

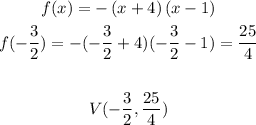
d) Finally, we can plot that function by setting a table:

So plotting these points (-2,6),(-1,6), (0,4), (1,0),(2,-6) and opening down the parabola for a is -1 we can plot this: