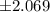Given
a). n = 4
b). n = 15
c). n = 24
Find
values that form the boundaries of the critical region for a two-tailed test with a = .05
Step-by-step explanation
a) n = 4
degree of freedom = n - 1 = 4 - 1 = 3
so , the t value for critical region =
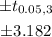
b) n = 15
degree of freedom = 15 - 1 = 14
so , t- value =
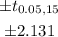
c) n = 24
degree of freedom = 24 - 1 = 23
so , t - value =
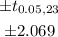
Final Answer
Hence , the values that form the boundaries of the critical region for a two-tailed test with a = .05 are
a)
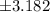
b)
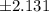
c)