We are given the following system of inequalities:
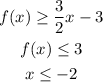
We are told to plot the graphs and find the coordinate of the vertices.
In order to find the vertices we need to plot each inequality.
Plot 1:
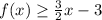
In order to plot this inequality, we simply choose two points because a line can be created with only two points.
The way to choose these two points, is to set x = 0 and find f(x) and set f(x) = 0 and find x. These would help us find the y-intercept and x-intercept respectively.
Let us perform this operation:
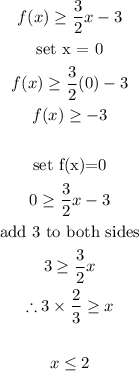
From the above, we just need to plot (0, -3) and (2, 0) to find the inequality plot.
We can see the forbidden region. This is the region that does not conform to the inequalities.
Next, we move to the next system of inequality.
Plot 2:
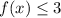
Here, we just draw the line f(x) = 3 and then shade the forbidden region as well.
The forbidden region here is above the line because that is the region where f(x) is greater than 3, hence we shade it off.
Finally, the last inequality:
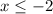
Plot 3:
We simply plot the line x = -2 and then shade the forbidden region
After plotting all three, we shall have the following:
j
The points V1, V2, and V3 where the lines meet are the coordinates of the vertices.
A picture of the vertices is attached below:
Thus, the vertices are (-2, 3), (4, 3) and (-2, -6)
The final answer is Option 2