Given
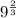
To write it in the simplest form and to find which value remains under the radical.
Step-by-step explanation:
It is given that,
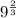
It is known that,
![x^{(m)/(n)}=\sqrt[n]{x^m}](https://img.qammunity.org/2023/formulas/mathematics/college/a00fqx3hetlbdzcyq207n389q0kknout01.png)
That implies,
![\begin{gathered} 9^{(2)/(3)}=\sqrt[3]{9^2} \\ =\sqrt[3]{3*3*3*3} \\ =3\sqrt[3]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/zsj60famy6k8o4192k61pyz4vkmvg8jg54.png)
Therefore, the simplest form of the expression is,
![3\sqrt[3]{3}](https://img.qammunity.org/2023/formulas/mathematics/college/igi91omwqz2el7p2fa5r3mb7amz6qfkgli.png)
and the value that remains under the radical is 3.