Answer: the percent yield of the reaction is 30.7%
Step-by-step explanation:
The question requires us to determine the percent yield of the reaction that produces copper(I) sulfide, given the theoretical yield and actual yield.
The following information was provided by the question:
Amount of Cu used = 0.0970 mol of Cu
Actual yield of reaction = 2.37 g of Cu2S
To solve this problem, we'll need to determine the theoretical yield of the reaction, considering the amount of copper (Cu) used and the balanced chemical equation for this reaction, and then calculate the percent yield of the reaction.
1) Determining the theoretical yield of reaction:
The reaction between copper and sulfur to produce copper (II) sulfide can be written as:
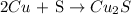
Considering that 0.0970 moles of Cu were used in excess of S, and the stoichiometry of the reaction, we can calculate the amount of Cu2S produced:
2 mol Cu ---------------------- 1 mol Cu2S
0.0970 mol Cu ------------ x
Solving for x, we have that 0.0485 moles of Cu2S should be obtained from the reaction.
2) Calculating the percent yield of the reaction:
The percent yield of a chemical reaction can be calculated using the following equation:
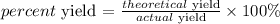
Note that the theoretical and actual yield values must be used in the same units. Thus, we need to convert the mass given for actual yield (2.37g) to number of moles, considering the molar mass of copper (I) sulfide (159.16 g/mol):
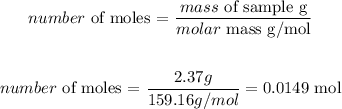
Therefore, the actual yield corresponds to 0.0149 moles of Cu2S.
Now, we can calculate the percent yield of the reaction:
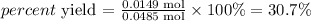
Therefore, the percent yield of the reaction is 30.7%.