Let the units place digit be U and the tens place digit be T.
The number N is given by:
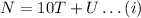
The number K is given by:
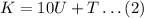
It is given that N is even that means U can be only from 0,2,4,6,8.
It is also given that N exceeds K by more than 50 so it follows:
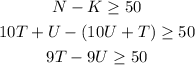
So it can be said that:
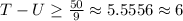
Since the value of T-U will always be an integer and it should be greater than or equal to 6.
The number T can be 1 to 9 and U can be only 0,2,4,6,8 so it follows:
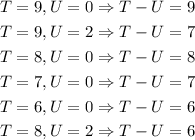
Hence the possible values for integer N are 90,92,80,70,60,82 and the respective integer K will be 09,29,08,07,06,28.
In all cases the difference is more than 50 as you can check.