Question

Solve. Show all your work!The digits of a positive two-digit integer N are interchanged to form an integer K. Find allpossibilities for N if N is even and exceeds K by more than 50.

Answer 1

Let the units place digit be U and the tens place digit be T.

The number N is given by:

`N=10T+U\ldots(i)`

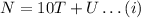
The number K is given by:

`K=10U+T\ldots(2)`

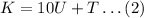
It is given that N is even that means U can be only from 0,2,4,6,8.

It is also given that N exceeds K by more than 50 so it follows:

`\begin{gathered} N-K\ge50 \\ 10T+U-(10U+T)\ge50 \\ 9T-9U\ge50 \end{gathered}`

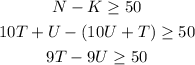
So it can be said that:

`T-U\ge(50)/(9)\approx5.5556\approx6`

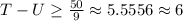
Since the value of T-U will always be an integer and it should be greater than or equal to 6.

The number T can be 1 to 9 and U can be only 0,2,4,6,8 so it follows:

`\begin{gathered} T=9,U=0\Rightarrow T-U=9 \\ T=9,U=2\Rightarrow T-U=7 \\ T=8,U=0\Rightarrow T-U=8 \\ T=7,U=0\Rightarrow T-U=7 \\ T=6,U=0\Rightarrow T-U=6 \\ T=8,U=2\Rightarrow T-U=6 \end{gathered}`

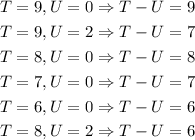
Hence the possible values for integer N are 90,92,80,70,60,82 and the respective integer K will be 09,29,08,07,06,28.

In all cases the difference is more than 50 as you can check.