Question

How do I solve this problem? String one is 5kg String 2 is 11 kg

Answer 1

ANSWERS

• Forces on the 5kg block: ,3

,

• Forces on the 11kg block: ,2

,

• Forces balanced? ,Yes, the system is at rest.

,

• Tension in string 1:

,

• Tension in string 2: ,107.91 N

Step-by-step explanation

First we have to draw the forces on each block:

Hence, block 1 has 3 forces acting on it, while block 2 has 2 forces acting on it.

It is said that the system is at rest, which means that the forces on the system are balanced.

By Newton's second law we know that,

`F_(t1)-F_(t2)-F_(g1)=0`

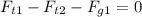
And,

`F_(t2)-F_(g2)=0`

Both equal zero because the blocks are not moving, and therefore there's no acceleration.

From the second equation we can find the tension in string 2,

`\begin{gathered} F_(t2)=F_(g2) \\ F_(t2)=m_2\cdot g \end{gathered}`

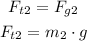
m2 = 11kg and g = 9.81m/s²,

Now that we know that the tension in string 2 is 107.91N, we can find the tension in string 1 replacing this into the first equation and solving for Ft1,

`F_(t1)=F_(t2)+F_(g1)`