We have to find 5 points of the parabola:
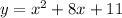
and then graph it.
We can find the vertex by completing the square:
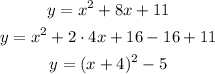
As we now have the vertex form of the parabola, we can see that the vertex is at (x,y) = (-4,-5).
We can now calculate two points to the right of the parabola by giving values to x as x = 0 and x = -2:
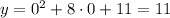
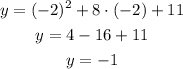
We now know two points to the right of the parabola: (0, 11) and (-2, -1).
As the line x = -4 is the axis of symmetry, we will have the same value for y when the values of x are at the same distance from this line.
Then, we can write:
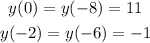
Then, we have two points to the left: (-8, 11) and (-6, -1).
We can graph the parabola as: