Question

Marco wants to take a taxi cab ride if the cost to ride is 7.00 with the cost per m is 0.25 per mile and mr. o can only spend 30 write linear inequality that model

Answer 1

Each ride has a fixed cost of 7 and a cost that increases proportionally to the distance travelled of 0.25 per mile. Therefore the total cost of the ride is:

`\text{ cost(x)}=0.25\cdot x+7`

Where "x" is the distance in miles. Marco can only spend 30 on his ride, therefore the cost must be less or equal to that value.

`\begin{gathered} \text{ cost(x)}\leq30 \\ 0.25\cdot x+7\leq30 \end{gathered}`

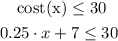
We can solve the linear equation by isolating the "x" variable on the left side.

`\begin{gathered} 0.25\cdot x\leq30-7 \\ 0.25\cdot x\leq23 \\ x\leq(23)/(0.25) \\ x\leq92 \end{gathered}`

Marco's travel must be shorter or equal to 92 miles.