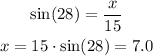Question

Can some one help me with 7 , 8 and 9 please?

Answer 1

7) The angle asked is ajacent to the leg given and we also have the hypotenuse. So we can use cossine:

`\begin{gathered} \cos x=(8)/(18)=(4)/(9) \\ x=\arccos ((4)/(9))=64\degree \end{gathered}`

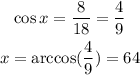
8) Here we want the hypotenus given an angle an its opposite leg. So we can use sine:

`\begin{gathered} \sin (65\degree)=(10)/(x) \\ x=(10)/(\sin (65\degree))=11.0 \end{gathered}`

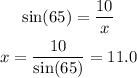
9) We want the leg which is opposite of a given angle and we have the hypotenuse. So we can use sine again:

`\begin{gathered} \sin (28\degree)=(x)/(15) \\ x=15\cdot\sin (28\degree)=7.0 \end{gathered}`