Question

Suppose cos(0) = -3/7 and 0 is in quadrant 2. What is the value of sin(0)?

Answer 1

In the second quadrant, the sine function is positive while the cosine function is negative.

`\Rightarrow\cos \theta<0,\sin \theta>0`

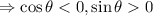
Furthermore, we can use the following trigonometric identity.

`\cos ^2\theta+\sin ^2\theta=1`

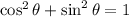
Therefore,

`\begin{gathered} \Rightarrow\sin ^2\theta=1-\cos ^2\theta \\ \Rightarrow\sin \theta=\pm\sqrt[]{1-\cos ^2\theta} \\ \Rightarrow\sin \theta=\sqrt[]{1-\cos^2\theta} \end{gathered}`

Because sin(theta) has to be positive, as stated before; thus,

`\begin{gathered} \Rightarrow\sin \theta=\sqrt[]{1-(-(3)/(7))^2}=\sqrt[]{1-(9)/(49)}=\sqrt[]{(40)/(49)}=\frac{\sqrt[]{40}}{7}=\frac{2\sqrt[]{10}}{7} \\ \Rightarrow\sin \theta=\frac{2\sqrt[]{10}}{7} \end{gathered}`

Thus, the answer is sinθ=2sqrt(10)/7