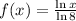Question

starting with the graph of f(x)=8^x write the equation of the graph that results from Shifting f(x) 5 units upward y=____shifting f(x) 9 units to the left y=____reflecting f(x) about the x axis and the y axis y=

Answer 1

We have the following:

`f(x)=8^x`

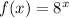
(a)

for there to be an upward displacement, we must add the function the value that we want it to rise, like this

`f(x)=8^x+5`

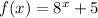
(b)

for there to be a shift to the left, we must add the exponent from the value we want it to rise, like this

`f(x)=8^(x+9)`

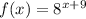
(c)

for there to be a shift to the left, we must subtract the exponent from the value we want it to rise, like this

The inverse is:

`\begin{gathered} y=8^x \\ x=8^y \\ \ln x=y\cdot\ln 8 \\ y=(\ln x)/(\ln 8) \end{gathered}`

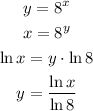
The answer is

`f(x)=(\ln x)/(\ln 8)`