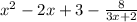
1) Since the degree of the denominator is lower than the numerator's we can divide these expressions through long division that way:
As we can see in each step the aim is to cancel the leading coefficient.
2) Note that a Long Division, has a way to write its answer so we can tell that this is the answer:
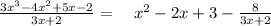
Note that the remainder is written above the divisor on the final answer.