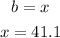Question

Solving right triangle find the missing side. round to the nearest tenth number 15

Answer 1

To solve the triangle we are going to first find the measures of all the angles:

`\begin{gathered} A=47\text{\degree} \\ B=90\text{\degree}\Rightarrow\text{ Because is a right triangle} \\ A+B+C=180\text{\degree} \\ \text{Because the sum of the internal angles of a triangle is 180 degrees} \\ 47\text{\degree}+90\text{\degree}+C=180\text{\degree} \\ 137\text{\degree}+C=180\text{\degree} \\ \text{ Subtract 137\degree from both sides of the equation} \\ 137\text{\degree}+C-137\text{\degree}=180\text{\degree}-137\text{\degree} \\ C=43\text{\degree} \end{gathered}`

Now to find the measures of the sides you can use trigonometric ratios because it is a right triangle:

Side a: you can use the trigonometric ratio tan(θ)

`\tan (\theta)=\frac{\text{ opposite side}}{\text{adjacent side}}`
`\begin{gathered} \tan (47\text{\degree})=(a)/(28) \\ \text{ Multiply by 28 from both sides of the equation} \\ \tan (47\text{\degree})\cdot28=(a)/(28)\cdot28 \\ 30=a \end{gathered}`

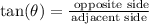
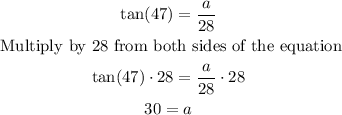
Side b or side x: you can use the trigonometric ratio cos(θ)

`\cos (\theta)=\frac{\text{adjacent side}}{\text{hypotenuse}}`
`\begin{gathered} \cos (47\text{\degree})=(28)/(b) \\ \text{ Multiply by b from both sides of the equation} \\ \cos (47\text{\degree})\cdot b=(28)/(b)\cdot b \\ \cos (47\text{\degree})\cdot b=28 \\ \text{ Divide by cos(47\degree) from both sides of the equation} \\ \frac{\cos (47\text{\degree})\cdot b}{\cos (47\text{\degree})}=\frac{28}{\cos (47\text{\degree})} \\ b=\frac{28}{\cos(47\text{\degree})} \\ b=41.1 \end{gathered}`

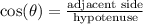
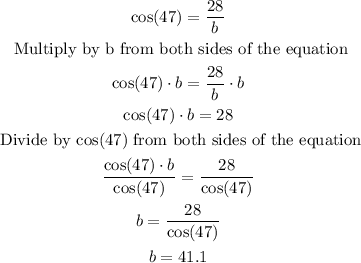
Therefore, when solving the triangle you have

`\begin{gathered} A=47\text{\degree} \\ B=90\text{\degree} \\ C=43\text{\degree} \\ a=30 \\ b=41.1 \\ c=28 \end{gathered}`

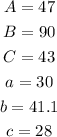
and the missing side is

`\begin{gathered} b=x \\ x=41.1 \end{gathered}`