Given,
The initial sale is 15.
The rate of increase of sale per week is 18 %.
The final sale is 1000.
The week at which the sales exceeds 1000 is:
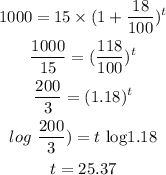
The sales of the business reach to 1000 in 25th week.
Hence, the sales of the business exceed to 1000 in 26th week.