From the given question
There are given that the matrix.
Now,
To find the inverse of any matrix, first find their determinant.
Then,
According to the properties of the matrix:
If the determinant of any matrix is zero, then their inverse has undefined.
So,
From the determinant of the given matrix:
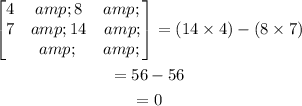
The determinant of the given matrix is zero
So, their inverse has not been defined.
Hence, the correct option is A.