Question

I am thinking of a number. It has two digits. When I reverse the digits and then add the new number to the original number I get 33. What is the number?

Answer 1

Let x and y be the digits.

The original number has two digits that means that one is the tens and the other the ones, in this case let x be the tens and y the ones, then we have the number:

`10x+y`

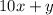
if we reverse it this means that the y become the tens and x becomes the ones then we have the number:

`10y+x`

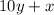
And if we add them the result is 33, then we have the equation:

`\begin{gathered} (10x+y)+(10y+x)=33 \\ 11x+11y=33 \\ x+y=3 \\ y=3-x \end{gathered}`

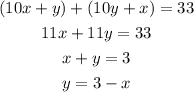
This means that y has to be 3-x. Now, since we both numbers to have two digits x can't be zero nor 3. Then has to be 1 or 2.

If x=1 then y=2 and the original number is 12.

If x=2 then y=1 and the original number is 21.

Notice how in both cases we get the other one when reversed, therefore the numbers we are looking for are 12 and 21.