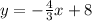Question

What is an equation of the line that passes through the points (6,0) and (3, 4)?

Answer 1

The slope-intercept form of the equation of a straight line is given to be:

`y=mx+b`

where m is the slope and b is the intercept on the y-axis.

The slope is calculated using two points on the line by the formula:

`m=(y_2-y_1)/(x_2-x_1)`

Therefore, for this line, the slope will be:

`m=(4-0)/(3-6)=-(4)/(3)`

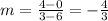
Therefore, this value for the slope is substituted back into the equation for the line:

`y=-(4)/(3)x+b`

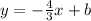
At the point (6, 0), we can calculate the value of b to be:

`\begin{gathered} 0=-(4)/(3)(6)+b \\ b=(4)/(3)(6) \\ b=8 \end{gathered}`

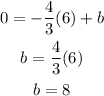
Therefore, the equation is:

`y=-(4)/(3)x+8`