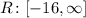1 Answer

Omid Ariyan · Answer 1 · 2023-11-10T07:43:30+0000

To find the vertex (h,k), we have to find h using the following formula

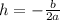
Where a = 1 and b = -10.

$h=-(-10)/(2\cdot1)=5$

Then, we find k by evaluating the function when x = 5.

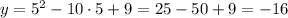
$y=5^2-10\cdot5+9=25-50+9=-16$

Hence, the vertex is (5,-16).

The axis of symmetry is given by the h coordinate of the vertex.

The y-intercept is found when x = 0.

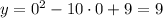
$y=0^2-10\cdot0+9=9$

The x-intercepts are found when y = 0.

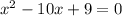
To solve this expression, we have to look for two numbers which product is 9, and which addition is 10. Those numbers are 9 and 1.

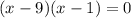
Then, we use the zero product property to express both solutions

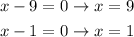
$\begin{gathered} x-9=0\rightarrow x=9 \\ x-1=0\rightarrow x=1 \end{gathered}$

The minimum value is defined by the k coordinate of the vertex.

The domain of the function would be all real numbers because quadratic functions don't have any domain restrictions.

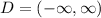
$D=(-\infty,\infty)$

The range of the function is determined by the vertex, given that the parabola opens upwards, then the range is

$R\colon\lbrack-16,\infty\rbrack$