The Solution:
Given the sequence below:
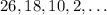
We are required to identify the type of sequence and to find the explicit rule for the given sequence.
Step 1:
To determine the type of sequence, we shall run the following check:

So,

Thus, the sequence is an arithmetic sequence.
Step 2:
To find the explicit rule, we shall use the formula below:

In this case,
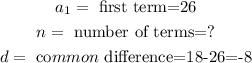
Substituting these values in the formula, we get

Therefore, the explicit rule of the sequence is :
