We have to calculate the water remaining in A after B is complete.
This will be equal to the volume of A minus the volume of B.
The volume of each cylinder is equal to the area of the base times the height, so we can calculate this difference as:
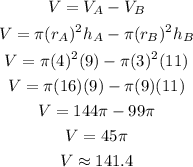
Answer: the remaining volume is approximately 141.4 cubic feet.