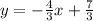Question

use the point slope formula in the given points to choose the correct linear equation in slope intercept formfor ( 4,-3) and (-2,5)

Answer 1

The point-slope formula is

`y-y_1=m(x-x_1)`

where m is the slope of a line passing through the point (x₁, y₁).

Also, the slope m of a line passing through points (x₁, y₁) and (x₂, y₂) is

`m=(y_2-y_1)/(x_2-x_1)`

In this problem, the line passes through points (4, -3) and (-2, 5). Thus, we have:

x₁ = 4

y₁ = -3

x₂ = -2

y₂ = 5

Then, the slope is

`m=(5-(-3))/(-2-4)=(5+3)/(-6)=(8)/(-6)=-(4)/(3)`

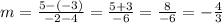
And the equation in point-slope form is

`y-(-3)=-(4)/(3)(x-4)`

Now, we need to rewrite this equation in slope-intercept form. The slope-intercept equation of a line with slope m and y-intercept b is

`y=mx+b`

Thus, we need to isolate y on the left side of the equation to obtain the slope-intercept form, as follows:

`\begin{gathered} y+3=-(4)/(3)x-(4)/(3)(-4)\text{ using the distributive property of multiplication over addition} \\ \\ y+3=-(4)/(3)x+(16)/(3) \\ \\ y+3-3=-(4)/(3)x+(16)/(3)-3 \\ \\ y=-(4)/(3)x+(16)/(3)-(9)/(3) \\ \\ y=-(4)/(3)x+(7)/(3) \end{gathered}`

Therefore, the slope-intercept form of that linear equation is

`y=-(4)/(3)x+(7)/(3)`