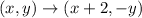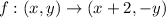1 Answer

Mitja Bonca · Answer 1 · 2023-03-19T16:46:37+0000

Given:

The pre-image coordinates (0, 5), (-3, 2), (4, -1) and transformed image coordinates (2, -5), (-1, -2), (6, 1).

Required:

We need to find the transformation in function notation.

Step-by-step explanation:

Let (x,y) be the pre-image coordinate and (x',y') be the transformed image coordinates.

The transformation is

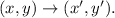
$(x,y)\rightarrow(x^(\prime),y^(\prime)).$

Consider the points (0,5) and (2,-5).

Substitute the values in the transformation.

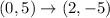
$(0,5)\rightarrow(2,-5)$

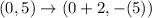
$(0,5)\rightarrow(0+2,-(5))$

Let x =0 and y =5, we get

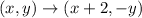
$(x,y)\rightarrow(x+2,-y)$

Consider the points (-3,2) and (-1,-2).

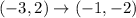
$(-3,2)\rightarrow(-1,-2)$
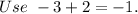
$Use\text{ }-3+2=-1.$

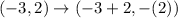
$(-3,2)\rightarrow(-3+2,-(2))$

Let x =-3 and y=2.

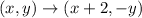
$(x,y)\rightarrow(x+2,-y)$

Consider the points (4,-1) and (6,-1).

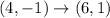
$(4,-1)\rightarrow(6,1)$
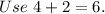
$Use\text{ }4+2=6.$

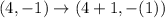
$(4,-1)\rightarrow(4+1,-(1))$

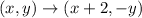
$(x,y)\rightarrow(x+2,-y)$

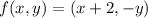
Final answer:

$(x,y)\rightarrow(x+2,-y)$

$f:(x,y)\rightarrow(x+2,-y)$

Please log in or register to add a comment.