Question

The perimeter of a rectangle is 32 meters and the length is 4 meters longer than width

Answer 1

Given:

The perimeter of a rectangle is 32 meters and the length is 4 meters longer than the width

Let, x = the length of the rectangle

And, y = the width of the rectangle

So, we have the following system of equations:

`\begin{gathered} 2x+2y=32\rightarrow(1) \\ x-y=4\rightarrow(2) \end{gathered}`

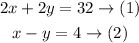
We will use the method of substitution to solve the system

So, from equation 2:

`x=y+4\rightarrow(3)`

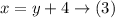
substitute with (x) from equation (3) intp eqaution (1)

`2(y+4)+2y=32`

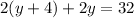
solve the equation to find (y):

`\begin{gathered} 2y+8+2y=32 \\ 4y+8=32 \\ 4y=32-8 \\ 4y=24 \\ y=(24)/(4)=6 \end{gathered}`

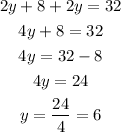
Now, substitute with (y) into equation (3) to find (x):

`x=y+4=6+4=10`

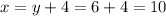
So, the answer will be:

The length of the rectangle = 10 m

The width of the rectangle = 6 m