Question

I need all solved, As soon as possible Question 1

Answer 1

Given:

`f(x)=3^x`

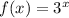
To find:

The type of function by completing the table and graphing the function

Step-by-step explanation:

When x = -2,

`\begin{gathered} y=3^(-2) \\ =(1)/(3^2) \\ =(1)/(9) \\ =0.11 \end{gathered}`

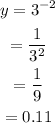
When x = -1,

`\begin{gathered} y=3^(-1) \\ =(1)/(3) \\ =0.33 \end{gathered}`

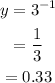
When x = 0,

`\begin{gathered} y=3^0 \\ =1 \end{gathered}`

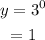
When x = 1,

`\begin{gathered} y=3^1 \\ =3 \end{gathered}`

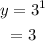
When x = 2,

`\begin{gathered} y=3^2 \\ =9 \end{gathered}`

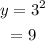
Therefore, the table values are,

Then, the graph will be,

Since the domain of the function is real numbers and the range of the function is a set of positive real numbers.

Therefore, it is an exponential function.