We want to find the equation of the line that passes through the points:
(4 , -8) and (9 , 11)
First, we're going to find the slope between these points using the fact that:
If we have two points that lie on a line:
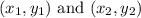
The slope between them can be found using the formula:

If we replace our values:
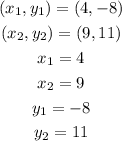
The slope will be:
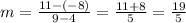
Now, we could apply the point-slope equation. This equation tells us that we can find the equation of the line if we got a point (x1,y1) on the line, and the slope m:
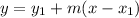
Replacing our values:
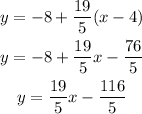
This, is the general form. We want to express the last equation as a standard form like this:
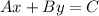
If we re-write:

Therefore, the standard for the equation of the line that passes through (4 , -8) and (9, 11) is:
19x-5y=116