Question

A table of 5 students has 2 seniors and 3 juniors. The teacher is going to pick 2 students at random from this group to present homework solutions. Find the probability that both students selected are juniors

Answer 1

`\text{ P\lparen both students are junior\rparen = }(1)/(10)`

Step-by-step explanation

Given information

The total number of junior students = 2

The total number of senior students = 3

The total number of students = 5

To determine the probability of picking two junior students, follow the steps below

Step 1: Define probability

`\text{ Probability = }\frac{\text{ possible outcome}}{\text{ total outcome}}`

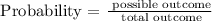
Step 2: Find the probability of picking the first junior students

`\begin{gathered} \text{ Probability = }\frac{possible\text{ outcome}}{total\text{ outcome}} \\ \text{ Probability of picking the first junior students is} \\ \text{ P\lparen Junior student\rparen = }(2)/(5) \end{gathered}`

Assuming the first picking was successful, then, we will be left with 1 junior student and 3 senior students.

Therefore, the new total outcome can be calculated below

1 + 3 = 4 students

Step 3: Find the probability that the second picking will be a junior student

`\begin{gathered} \text{ Probability = }\frac{\text{ possible outcome}}{\text{ total outcome}} \\ \text{ P\lparen picking the second junior student\rparen = }(1)/(4) \end{gathered}`

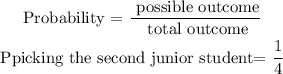
Step 4: Find the probability that both students are junior students

`\begin{gathered} \text{ P\lparen both students are junior students\rparen = }(2)/(5)*(1)/(4) \\ \text{ P\lparen both students are junior students\rparen = }(2)/(20) \\ \text{ P \lparen both students are junior students \rparen = }(1)/(10) \end{gathered}`

Hence, the probability that both students selected are juniors is 1/10