Given the graph of an inequality, you can identify that the boundary has the form of a "V". Therefore, you can identify that it is an Absolute Value Inequality.
By definition, an Absolute Value Equation written in Vertex Form is:
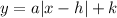
Where "h" is the x-coordinate of the Vertex, and "k" is the y-coordinate of the Vertex. If "a" is negative, the graph opens down and if it is positive, the graph opens up.
In this case, the graph opens up, and you can identify in the graph that the Vertex is:
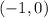
You can also identify that the boundary is formed by solid lines and the shaded region is below the boundary. This indicates that the inequality has this form:
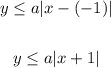
Notice that this inequality is given in the Answer choices:

In order to check it, let's choose two points on the shaded region:

Substitute the coordinates into the inequality and evaluate. If they satisfy the inequality, then the are solutions to it:
- For the first point:

- For the second point:
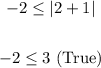
Hence, the answer is: Second option.