The slope is define as the rate of y coordinate with respect to the x coordinate.
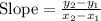
In the line D which is parallel to x axis has the constant y coordinate i.e
y = -3
So, for the numerator of the slop for line D is ( -3) - ( -3) = 0
Thus the slope will be express as :

Thus the slope of line is 0
Now, for the line A :
The line A is parallel to y axis, that is only y coorsinates are changes x is at contant position.
i.e. x = -5
So, substitute the value in the expression for the slope :
![\begin{gathered} \text{Slope}=(y_2-y_1)/(x_2-x_1) \\ \text{Slope}=\frac{y_2-y_1}{-5-(-5)_{}} \\ \text{Slope}=\frac{y_2-y_1}{-5+5_{}} \\ \text{Slope = }\frac{y_2-y_1}{0_{}} \\ If\text{ the denominater becomes zero, then the expression is not define} \\ So,\text{ slope of line A is not define} \end{gathered}]()
Slope of line A is not define
In the line B and C, the coordinates of x and y aixs are changes countinously
thus thier slopes will be well define.
Answer : Slope of line A is not define.