Answer:
a)
b)
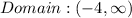
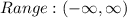
c) x-intercept is 0
Step-by-step explanation:
Given:
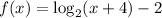
a) See below the graph of different transformations of the given function;
The equation of the vertical asymptote as shown on the graph is x = -4
b) The domain of a function is the set of possible input values for which the function is defined. The domain of a graph is the set of possible values from left to right.
Looking at the given graph, we can see that the domain of the function is;
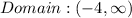
The range of a graph is the set of values from the bottom to the top of the graph. Looking at the graph, we can see that the range is;
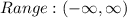
c) We'll follow the below steps to determine the x-intercept of the function;
Step 1: Substitute f(x) with 0;
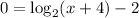
Step 2: Add 2 to both sides;
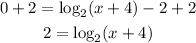
Step 3: Apply the below rule;
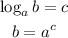
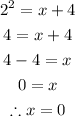
So the x-intercept is 0