Question

Section 5.2-12. Solve the following system of equations by substitution or elimination. Enter your answer as (x,y).3x-3y = -6-x+2y = 8

Answer 1

the Given the simultaneous equations

`\begin{gathered} 3x-3y=-6\text{ ------(1)} \\ -x+2y=8\text{ -------(2)} \end{gathered}`

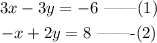
Solving the above equations by substitution method:

Step 1:

From equation 2, make x the subject of the formula

`\begin{gathered} -x+2y=8 \\ \text{making x the subject of formula, we have} \\ x=2y-8\text{ -------(3)} \end{gathered}`

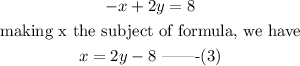
Step 2:

Substitute equation 3 into equation 1

Step 3:

Substitute the value of y in either equation 1 or 2.

`\begin{gathered} \text{From equation 2,} \\ -x+2y=8 \\ \text{Thus,} \\ -x+2(6)=8 \\ -x+12=8 \\ \text{collecting like terms, we have} \\ -x=8-12 \\ -x=-4 \\ x=4 \end{gathered}`

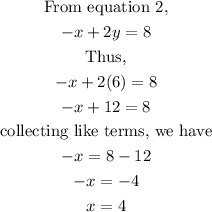
Thus, the values of (x, y) are (4, 6)