Here, from the figure we see that,
Line EI is parallel to HG.
And EH and GI act as the transversal lines for the given parallel pair.
So, we get
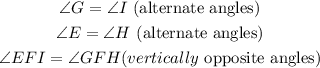
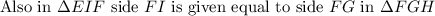
Therefore, we have two angles and one side equal in two triangles.
Henceproved that , they are congruent with the ASA (Angle Side Angle)rule.