Part A.
The composition of f ang g is given by
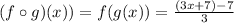
where we have inserted 3x-7 in the place of x in function f. Then, we have

Therefore, the answer is
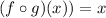
Part B
Similarly to the previous case, we have
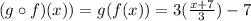
which gives
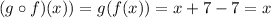
then, the answer is

Part C.
In the first case, x belongs to the domain of g and g(x) belongs to the domain of f. Then, the domain of the composition (fog)(x) is all real numbers.
Similarly, in the second case, x belongs to the domain of f and f(x) belongs to the domain of g. Then, the domain of the composition (gof)(x) is all real numbers. Then, the domains are the same (all real numbers).