Given
Values for relation g
Find
Which pair is in g inverse.
Step-by-step explanation
In the inverse function , it satisfies when y = f(x)
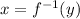
so , in the inverse of g
since g(4) = 9 , so
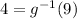
g(5) = 13 , so
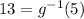
g(3) = 5 , so
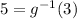
g(2) = 2 , so
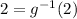
so , (13 , 5) would be found in the inverse of g
Final Answer
Hence , the correct option is (13 , 5)