Let's start by drawing the situation:
According to this, one of the dimensions of the box is 40-2x. The other one is 30-2x and the last one, that we could say it's the height, is x.
The volume of a box is given by the product of the three dimensions:
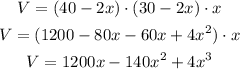
Use the given value of the volume to find x:

Factoring this expression we have that:
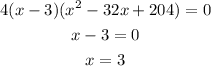
One of the possible dimensions of the square is 3. Now, solve the quadratic expression (third factor) to find the other 2 options:
![\begin{gathered} x^2-32x+204=0 \\ x=\frac{-(-32)\pm\sqrt[]{(-32)^2-4(1\cdot204)}}{2\cdot1} \\ x=\frac{32\pm\sqrt[]{1024-816}}{2} \\ x=\frac{32\pm\sqrt[]{208}}{2} \\ x1=\frac{32+\sqrt[]{208}}{2} \\ x2=\frac{32-\sqrt[]{208}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/g6x2rqpf2aub75hbqqbtpp4i7hexyoe6tz.png)
It means that the squares can have 3 different dimensions, which are:
![3,\frac{32+\sqrt[]{208}}{2},\frac{32-\sqrt[]{208}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/d8h49ulbwqkrnbrmnq4ebp7c620uagtpwt.png)
Nevertheless, the second possible option is not coherent since it's value is close to 23 and the dimensions of the cardboard are 30 and 40. It means that the possible dimensions are 3 and (32-sqrt(208))/2.