1 Answer

SMGreenfield · Answer 1 · 2023-03-05T02:03:29+0000

we have the functions

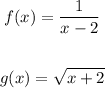
$\begin{gathered} f(x)=(1)/(x-2) \\ \\ g(x)=√(x+2) \end{gathered}$

Find out f(g(x))

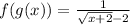
$f\mleft(g\mleft(x\mright)\mright)=(1)/(√(x+2)-2)$

Remember that

The radicand must be greater than or equal to zero and the denominator cannot be equal to zero

so

step 1

Solve the inequality

$\begin{gathered} x+2\ge0 \\ x\operatorname{\ge}-2 \end{gathered}$

the solution to the first inequality is the interval [-2, infinite)

step 2

Solve the equation

$\begin{gathered} √(x+2)-2\\e0 \\ √(x+2)\operatorname{\\e}2 \\ therefore \\ x\operatorname{\\e}2 \end{gathered}$

The domain is the interval

[–2, 2) ∪ (2, ∞)

Please log in or register to add a comment.