In this problem, we want to find the volume of a pyramid. In general, the formula for the volume of a pyramid is
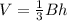
where B represents the base shape's area, and h represents the height.
From the image, we can see the base shape is a square, and we can use the formula:

Note: the area of a square is the side-length squared, and since we know the side length is labeled x, we can update the formula as we did above.
We are given x = 8 and y = 24, so we can substitute and simplify to find the volume:
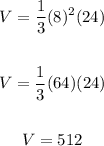
The final volume is 512 cubic units.