Given:
The slope of the line
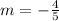
The line passes through from the point (5,3).
Required:
Find the equation of the line.
Step-by-step explanation:
The equation of the line that passes through from the point and has slope m is given by the formula as:

Consider
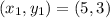
Now the equation of the line:
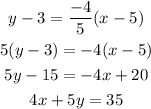
Final Answer:
The equation of the line passes through from point (5,3) and has a slope -4/5 is 4x + 5y = 35