Question

In a music class of 20 students, there are 12 who play the Guitar (G), 7 who play the piano (P) and 4 who do not play any of his instruments.A) Represent the situation using a Venn diagram.B) What is the probability that a randomly selected student will play guitar and piano?C) What is the probability that a randomly selected student will play one of these two instruments?D) What is the probability that a randomly selected student will not play the piano?

Answer 1

n(U) = 20

n(G) = 12

n(P) = 7

`\text{ n(G u P)}^1=4`

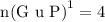
Let x represent students that play both instruments

n(PuG) = x

A. Venn diagram

B. What is the probability that a randomly selected student will play guitar and piano?

Firstly solve for x

12-x + x + 7-x + 4 = 20

23-x = 20

-x = 20 - 23

-x = -3

x = 3

Number of students that play guitar and piano = x = 3

Total students = 20

Probability that a randomly selected student will play guitar and piano = 3/20

C. What is the probability that a randomly selected student will play one of these two instruments?

`\begin{gathered} \text{ = }(12-x)/(20)\text{ +}(7-x)/(20) \\ =(12-3)/(20)+(7-3)/(20) \\ =(9)/(20)+(4)/(20) \\ =(13)/(20) \end{gathered}`

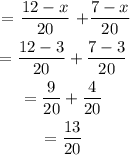
D. What is the probability that a randomly selected student will not play the piano?

Students who do not play piano are students that play guitar only and students who do not play any instrument

students that play guitar only = 12 -x = 12 -3 = 9 students

students who do not play any instrument = 4

Probability that a randomly selected student will not play the piano =

`(9)/(20)+(4)/(20)\text{ = }(13)/(20)`