Question

Which of the following sequences represents an arithmetic sequence with a common difference d = –4? 768, 192, 48, 12, 3 35, 31, 27, 23, 19 24, 20, 16, 4, 0 5, –20, 80, –320, 1,280

Answer 1

The general formula of an arithmetic sequence is:

`a_n=a_1+(n-1)\cdot d`

Where d is known as the common difference and it represents the distance between consecutive terms of the sequence. So we can calculate this distance for each of the four options:

`\begin{gathered} 768,192,48,12,3 \\ 768-192=576 \\ 192-48=144 \end{gathered}`

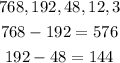
So in the first sequence the difference between terms is not even constant so this is not the correct option.

`\begin{gathered} 31-35=-4 \\ 27-31=-4 \\ 23-27=-4 \\ 19-23=-4 \end{gathered}`

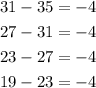
In the second sequence the distance is -4 so this is a possible answer.

`\begin{gathered} 20-24=-4 \\ 16-20=-4 \\ 4-16=-12 \\ 0-4=-4 \end{gathered}`

In the third sequence the distance is not always the same so we can discard this option.

`\begin{gathered} -20-5=-25 \\ 80-(-20)=100 \end{gathered}`

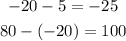
Here the distance isn't constant so the fourth option can also be discarded.

Then the only sequence with a distance d=-4 is the second option.